Arwanak, 5109
tags: grammar, linguistic spatiality, temporal sorcery, anexelentic kabbalah
Translating systems into SpaceLang
The first step of effective utilization of SpaceLang is to translate a given linguistic system into the SpaceLang schematic. This, for the English language at least, is done using an adapted gematric calculation based on the plurality of the three in space and time (Past, Future, Present), (Here, Near, Far). The gematric table also represents the inside and outside and the direct spatiality between them, which can be symbolically made into a triangle (3). The table below details the numerical correspondences of each letter in the English alphabet:
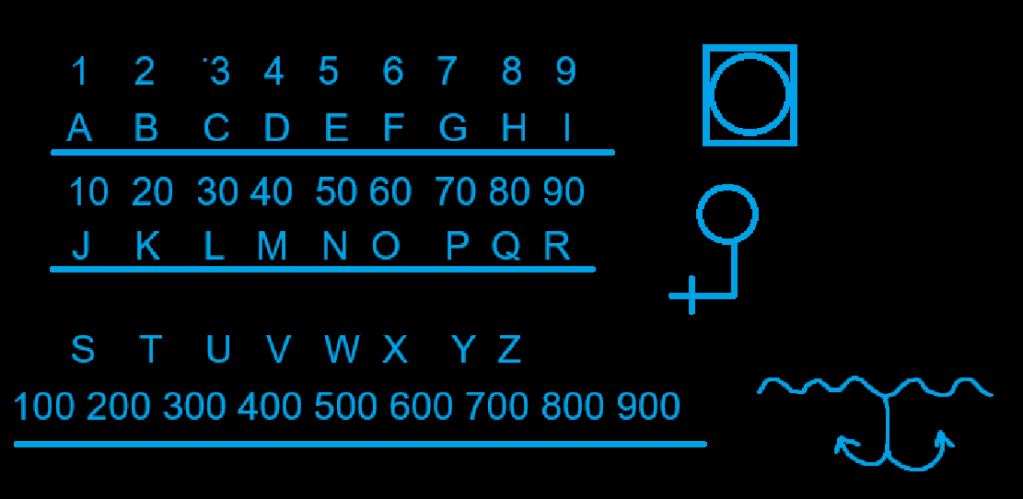
The first step is therefore to calculate a value for each a letter in a linguistic system. Our example sentence that we will translate is: “Undercutting is sacred.”. We find the numerical values on the table and then add them. Once a three digit or two digit number is calculated, it is then plexed into a single digit numerical value for that word. The calculations for the example sentence is thus:
1.
U+N+D+E+R+C+U+T+T+I+N+G= 300+50+4+5+90+3+300+200+200+9+50+7
1218=1+2+1+8
12=1+3
=3
2.
I+S=9+100
9+100=109
109=1+0+9
10=1+0
=1
3.
S+A+C+R+E+D=100+1+3+90+5+4
100+1+3+90+5+4=203
203=2+0+3
=5
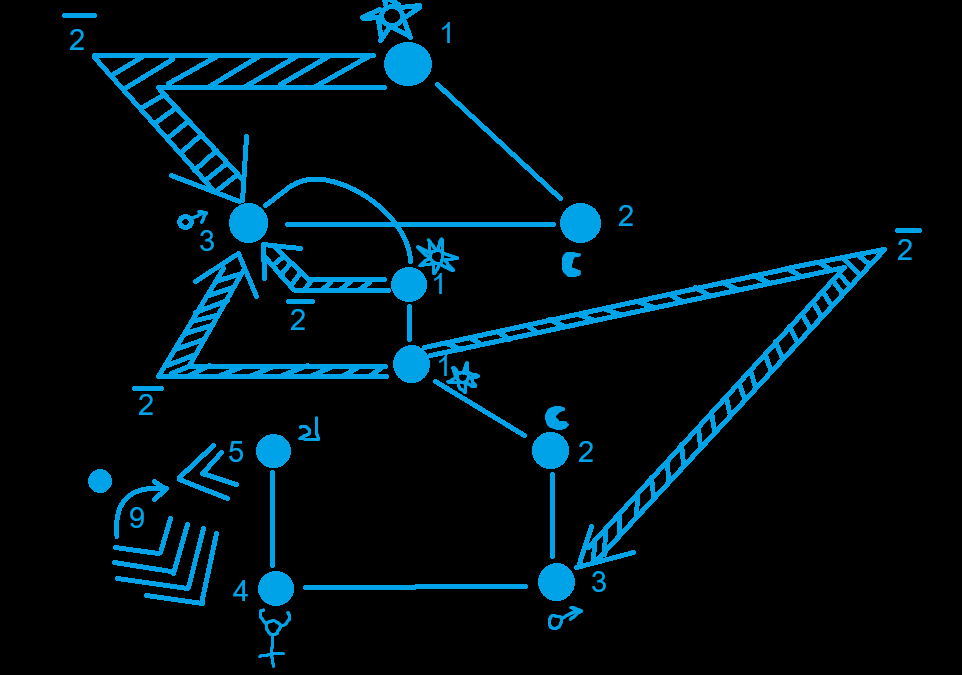
The sequence is (3,1,5) and the next step is to arrange it into a sequence of temporal planes corresponding to the order in which the sentence is spoken. Numbers are represented by geometric strictures in SpaceLang, analogous to the platonic solids in two dimensions. In our case the geometric symbols are (triangle, point, pentagon) arranged top-to-bottom, aligned with an abstract time-ordering of (Past, Present, Future).
The shapes are arranged in a two-dimensional manner, with points being referred to as nodes. Each node has a value on its own and is directly incorporated into the arrangement of time-distance, which the geometric shape arrangement has also been incorporated into. On a two-dimensional graph, lay out only the nodes of the system and assign numbers based on a simple n+1 counting. Upon the transition into a new plane, the counting resets back to 1.
Association between nodes is conducted in three primary linkages in SpaceLang. Those being L1, L2 and L3 links. L1 links are simple counting, based links that are represented with a line and they internally connect all the points on a given shape-plane. Once an ending is reached, the L1 link connects to node 1 in the next plane. L2 links are triangulators, and function as direct linkages between triangular numbers in the system. Those being nodes with numerical values of (1, 3, 6). L2 links are represented as an arrow with internal stripes. An imaginary triangulated value is also assigned to the turning point of the L2 link. For example, a link between nodes (1) and (3) is supplanted with a non-node of (2), completing the triangulation. L3 links exist as Outside links between nodes whose values add up to 9. They operate via a nexus, whose numerical value is determined as the sum of the connected nodes. As as an example, nodes (5) and (4) are linked via nexus (9) in all cases.
The final representation of “Undercutting is sacred” in SpaceLang functions as an abstract linguistic map of correspondences between numbers, time, space and symbols that can be used for aeonically sorcerous purposes. The final result is: